Mar 21, 2023
Author(s)
Large language models (LLMs) solve natural language processing problems with astounding accuracy. However, these models are enormous and require a lot of space, cost, and computation power to deploy. For example, the GPT-175B model has 175 billion parameters requiring 320GB of storage and at least 5 A100 GPUs with 80GB of memory each for inference. This computation power is expensive, making this solution only viable for some organizations. Hence, deployment of such models falls outside the purview of small organizations and individuals.
Several model compression techniques, such as quantization and pruning, have been proposed to compress LLMs. Previous solutions have required extensive retraining to recover lost accuracy. This retraining also requires massive computation power, which is not economical for real-world deployments. Therefore, a solution that can prune LLMs without retraining the model would be a game changer in deploying large language models. At the moment, it is estimated that it can take several weeks to prune a GPT3 model. Enter SparseGPT.
SparseGPT is a post-training pruning method for compressing large language models such as GPT3 efficiently and accurately. The method can be used to prune large language models in one-shot with minimal accuracy loss. For example, you can use SparseGPT to prune OPT-175B to 50% sparsity with a 0.13 decrease in perplexity.
Thus 100 billion weights from the model can be ignored at inference time, increasing the model's throughput while reducing latency. SparseGPT can be applied to a GPT model with 175B parameters on a single GPU in a couple of hours with negligible accuracy loss.
In this article, you will learn about the SparseGPT algorithm and how it works. By the end of the article, you will be familiar with how this method reduces the size of large language models, making it possible to deploy them efficiently on commodity CPUs.
Let’s dive in.
Methods For Pruning Large Language Models
To understand how SparseGPT works, you have to understand post-training pruning and layer-wise pruning.
Post-training pruning works by creating a compressed version of a model that satisfies a given compression predicate. The method has been used to reduce the computation cost of quantization-aware training. Existing post-training pruning work mostly focuses on CNN and transformer models with less than 100 million parameters. There is also existing work on quantization of large language models, but it mostly focuses on reducing the precision of the numerical representation of individual weights.
Layer-wise pruning splits the model compression problem into layer-wise subproblems. The quality of the solution is measured by the error between the output of the uncompressed and compressed layer by solving a constrained optimization problem. The objective is to find a sparsity mask for each layer that satisfies the constraint and the dense weights. The sparsity mask of a tensor is the binary tensor of the same dimensions with 0 at the indices of the sparsified entries and 1 at other indices. After solving each of the layer-wise problems, the model is rebuilt from the compressed layers. The reconstructed model preserves the accuracy of the dense model if the layer-wise errors are small.
Optimizing the sparsity mask and the weights jointly makes the problem NP-hard. Hence, solving this problem can only be done through approximations. AdaPrune has been proposed for post-training through magnitude-based weight selection and reconstruction of the remaining weights by applying SGD finetuning. Other methods such as Optimal Brain Compression, have also been proposed to remove weights one at a time and fully reconstruct the weights after each iteration. Unfortunately, these methods have a high runtime on LLMs. And this is where SparseGPT enters the scene.
How Does the SparseGPT Algorithm Work?
Assuming that a pruning mask is fixed, the update has a closed-form solution via the Hessian. The problem can be split into row-wise subproblems. Reconstructing pruned weights is a complex problem because it requires the inversion of a matrix while solving for each row, and the inverse of a masked Hessian is not equal to the masked version of the full inverse. This problem is referred to as the Row-Hessian challenge. The task would be easier if all row masks were the same (for example, if pruning happens column-wise), meaning that only a single shared inverse would be computed. Introducing such constraints in the mask selection would mean sparsifying weights in entire columns, which is difficult and reduces the model's accuracy. SparseGPT solves the row-hessian challenge by reusing Hessians between rows and distinct pruning masks, leading to an accurate and efficient algorithm.
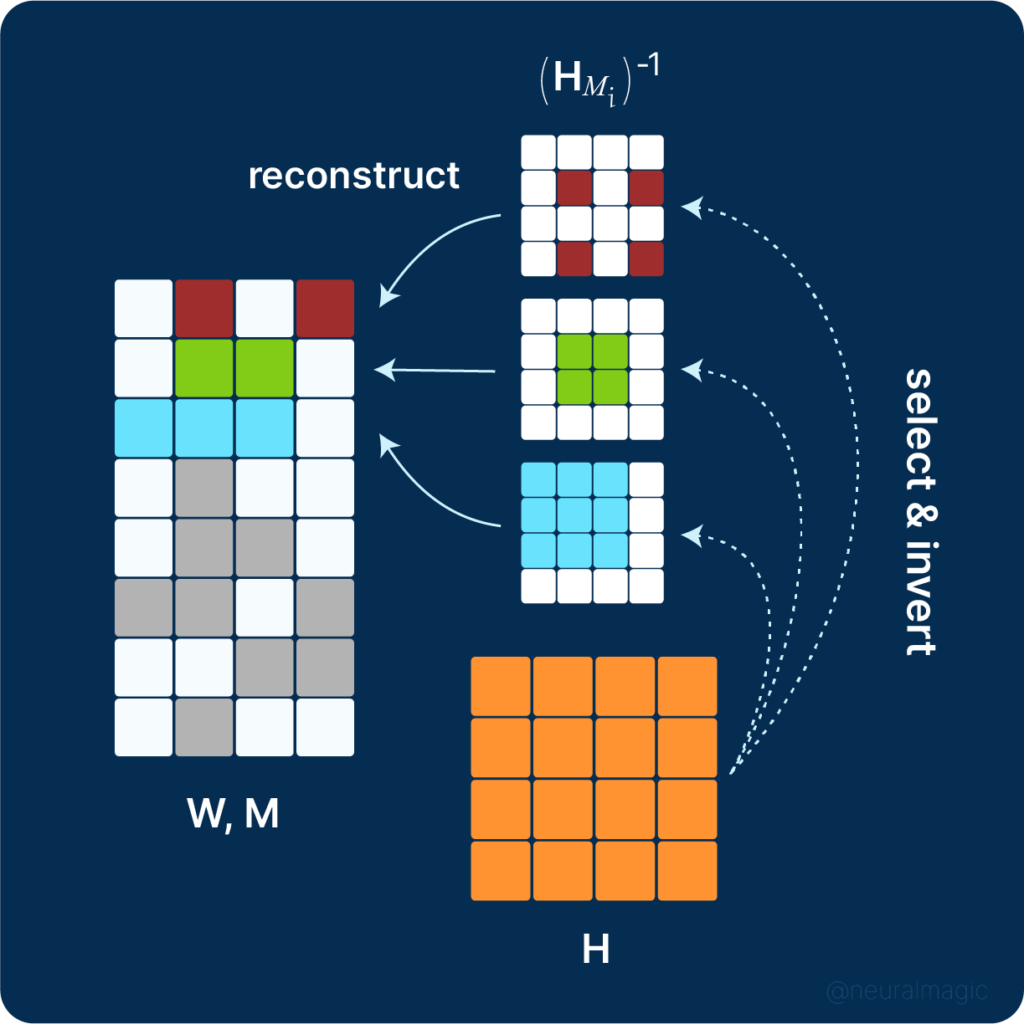
SparseGPT aims to prune large language models at a fraction of the cost and time spent by previous methods. This makes SparseGPT applicable to models with 100 billion parameters. It works by setting the weights not in the mask to 0 and setting the rest to their current value.
The SparseGPT algorithm works as follows, given a fixed pruning mask:
- Prune weights in each column of the weight matrix incrementally using a sequence of Hessian inverses
- Update the remainder of the weights in the rows located to the right of the column being processed
Pruned weights (blue) are updated to compensate for the pruning error, while unpruned weights (light blue) generate no updates.
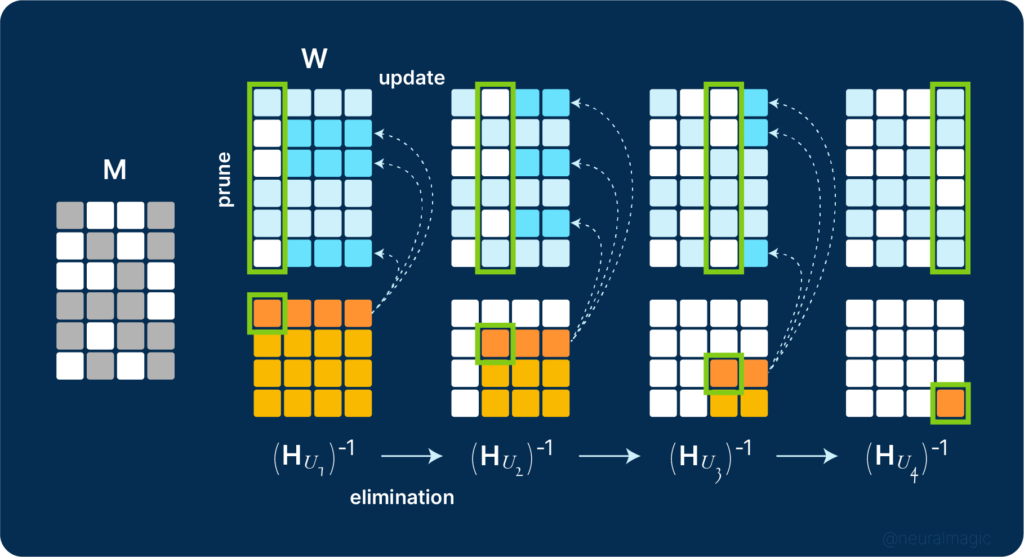
SparseGPT is local because it performs weight updates after each pruning step, maintaining the input-output relationship between each layer. The high parametrization of GPT models makes it possible to make the updates without any global gradient information. The cost of the reconstruction process consists of the computation of the initial Hessian, iterating through the inverse Hessian sequence, and pruning.
The pruning mask is chosen adaptively while performing the reconstruction process. This is done to reap the benefits adaptive weight selection offers during pruning. The selection is done through iterative blocking, where a pruning mask is chosen based on the reconstruction error while using the diagonal values in the Hessian sequence. The weights are then updated before the pruning mask for the next block is chosen. This is done iteratively, enabling non-uniform selection per column using the corresponding Hessian information and prior weight updates.
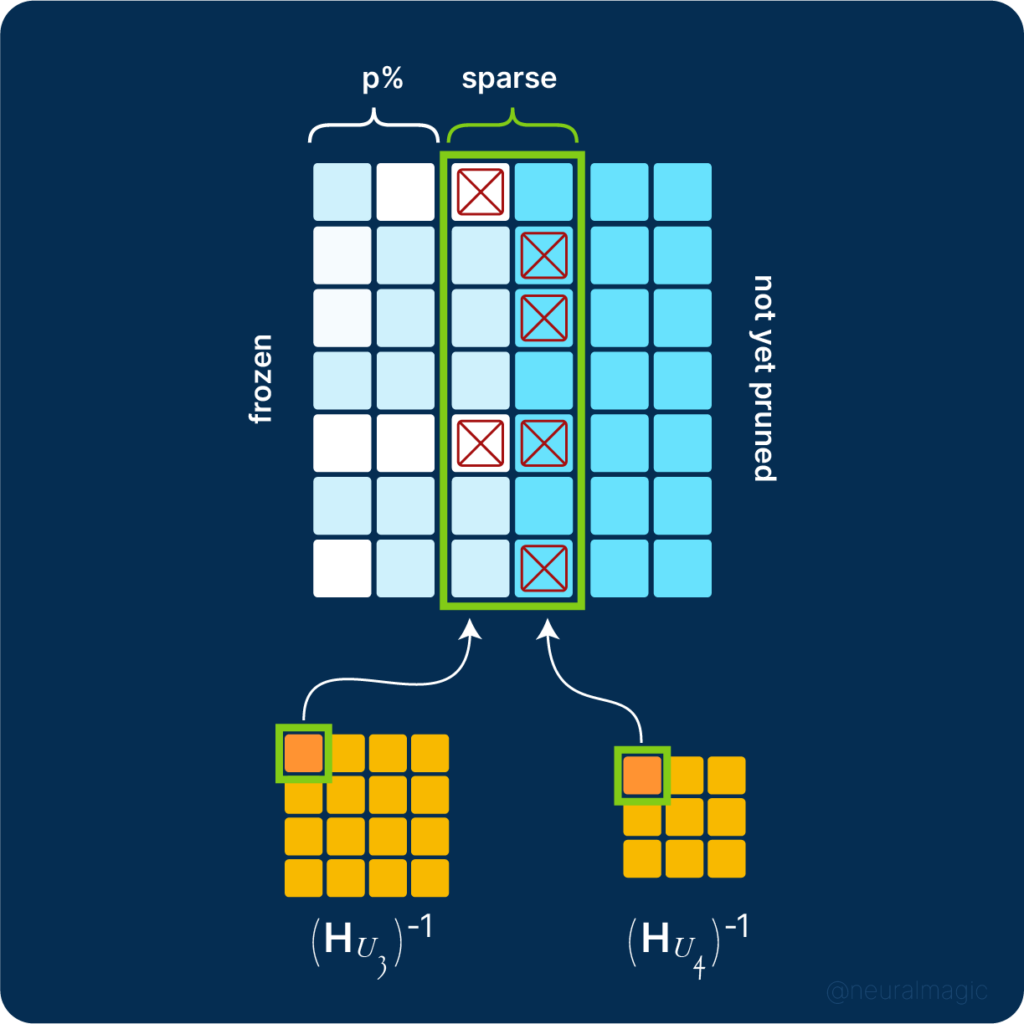
The SparseGPT algorithm pseudocode is shown below.

The pseudocode is interpreted as:
- Create a pruning mask M with zeros and ones.
- Construct a matrix E to store the block quantization errors.
- Calculate the inverse Hessian sequence information via Cholesky decomposition.
- Loop the blocks while updating the pruning mask and the error.
- Select the largest weights for each block and set their corresponding values in the pruning mask to 1.
- Prune the remaining weights and set their corresponding values in the pruning mask to 0.
- Compute the pruning error for each weight in the block and set the error in the E matrix.
- Freeze the weights that were not pruned.
- Update the weights in the block using the Cholesky decomposition of the inverse Hessian matrix.
- Update weights not updated in the previous loop after processing all the blocks.
- Set pruned weights to 0 by element-wise multiplying the weight matrix with the pruning mask.
SparseGPT is implemented in PyTorch using the Hugging Face Transformers library. Experiments on a single NVIDIA A100 GPU with 80GB of memory show that SparseGPT can fully sparsify 175-billion-parameter models in approximately 4 hours without fine tuning.
SparseGPT Evaluation
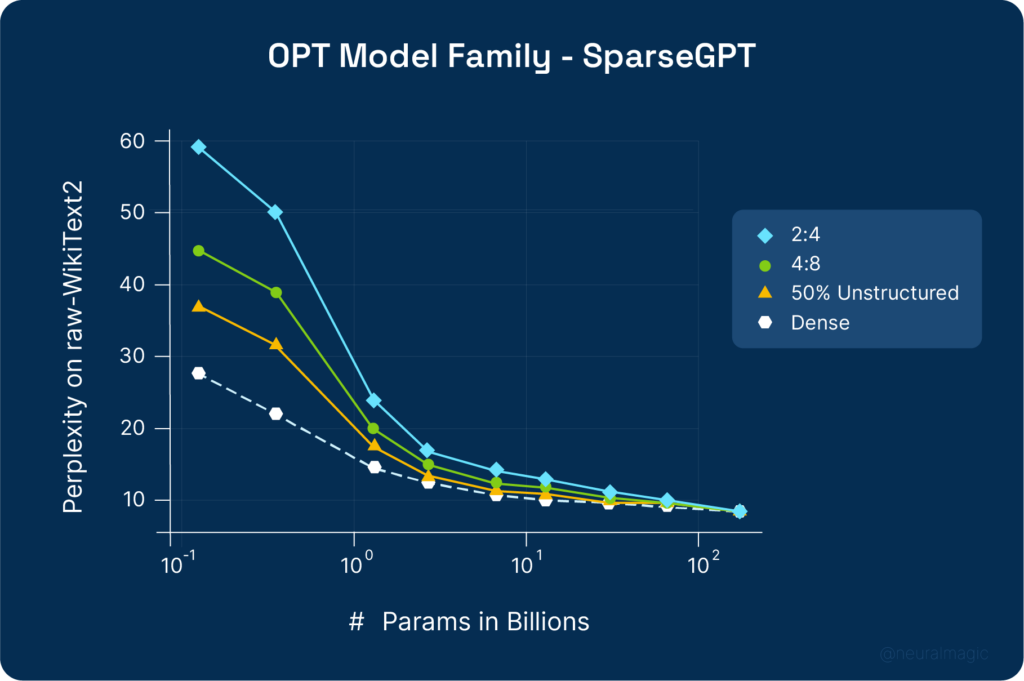
SparseGPT is evaluated using perplexity on the raw-WikiText2 test set, performing better than magnitude pruning.
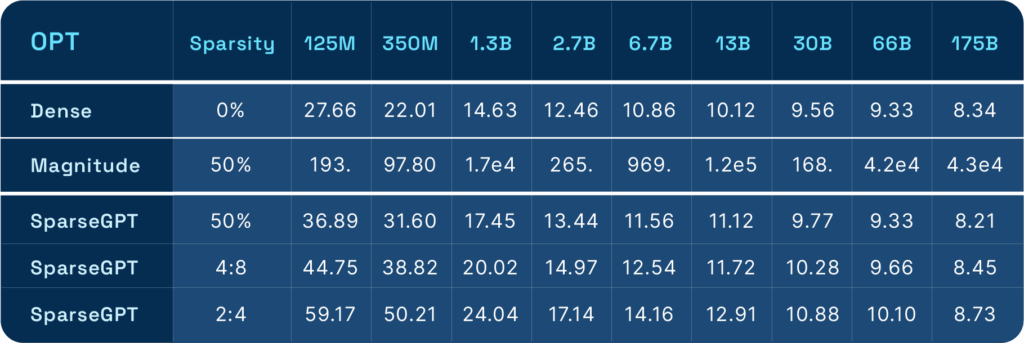
The researchers also evaluated SparseGPT and magnitude pruning on OPT-175B. The left graph shows how the performance of both methods scales with the degree of sparsity. Magnitude pruning achieves 10% sparsity, after which the model’s loss starts reducing, while SparseGPT enables up to 60% sparsity.
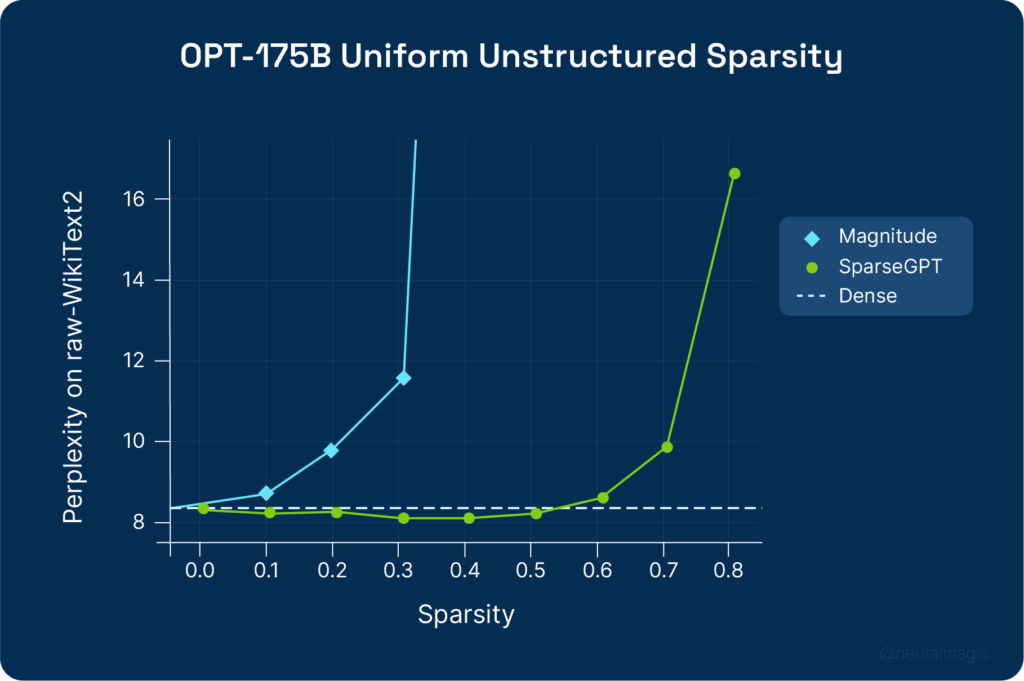
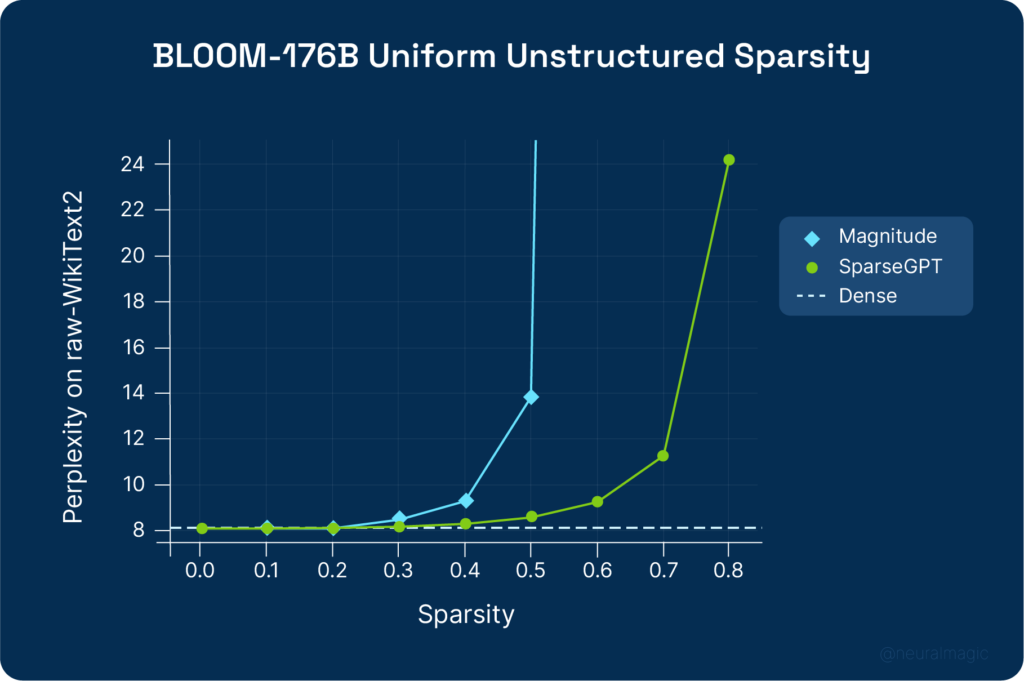
For BLOOM-176B, magnitude pruning achieves 30% sparsity and SparseGPT 50%. SparseGPT can remove 100 billion weights from BLOOM and OPT models without significant loss in accuracy.
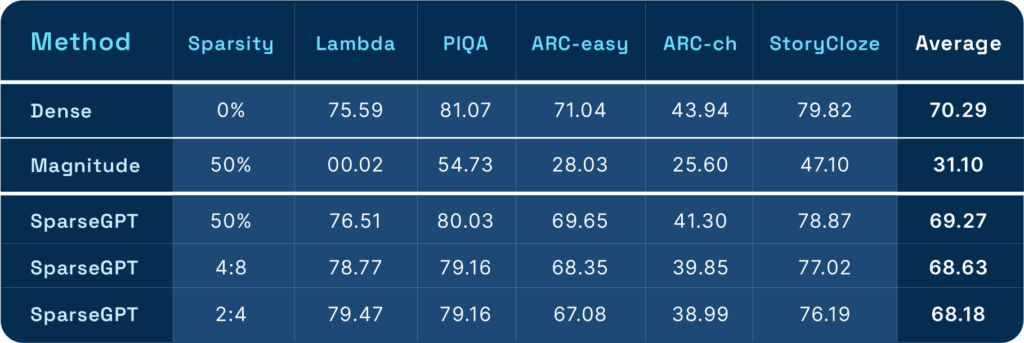
The researchers obtained the following results for ZeroShot experiments, showing that SparseGPT retains accuracy closer to the original while magnitude pruning doesn’t.
Final Thoughts
Amazingly, 100 billion parameters from large language models can be ignored at inference. This accomplishment paves the way for the broad usage of these models because of their lower computational and storage requirements. The researchers conjecture that fine-tuning the large models after pruning can lead to the recovery of more accuracy while allowing the models to be pruned between 80% and 90%.
At Neural Magic, we continue to push the envelope in making large language models generally available by providing models that have been pruned, hence ready to use, and providing the tools you need to prune and quantize your models. Join our community to interact with other deep learning practitioners and stay up to date with our work in optimizing large language models.
*Resource for all figures: "SparseGPT: Massive Language Models Can Be Accurately Pruned in One-Shot." arXiv, 19 January 2023, https://arxiv.org/pdf/2301.00774.pdf