Oct 14, 2024
Author(s)
Mixed-input quantization is a technique that processes weights and activations at different precisions in neural networks. The most common implementation is w4a16 quantization (e.g., GPTQ or AWQ), which uses 4-bit quantized weights and 16-bit activations (float16 or bfloat16). This approach primarily aims to reduce GPU memory requirements for model execution.
In most Large Language Model (LLM) workloads, model weights consume the majority of GPU memory. By quantizing weights from float16 to 4-bit, a remarkable ~4x reduction in memory needed for weight storage can be achieved. Additionally, smaller weights can lead to speedups when the linear layer is memory-bound (i.e., limited by weight loading), which occurs when the batch or sequence length is small, resulting in activations being much smaller than the weights.
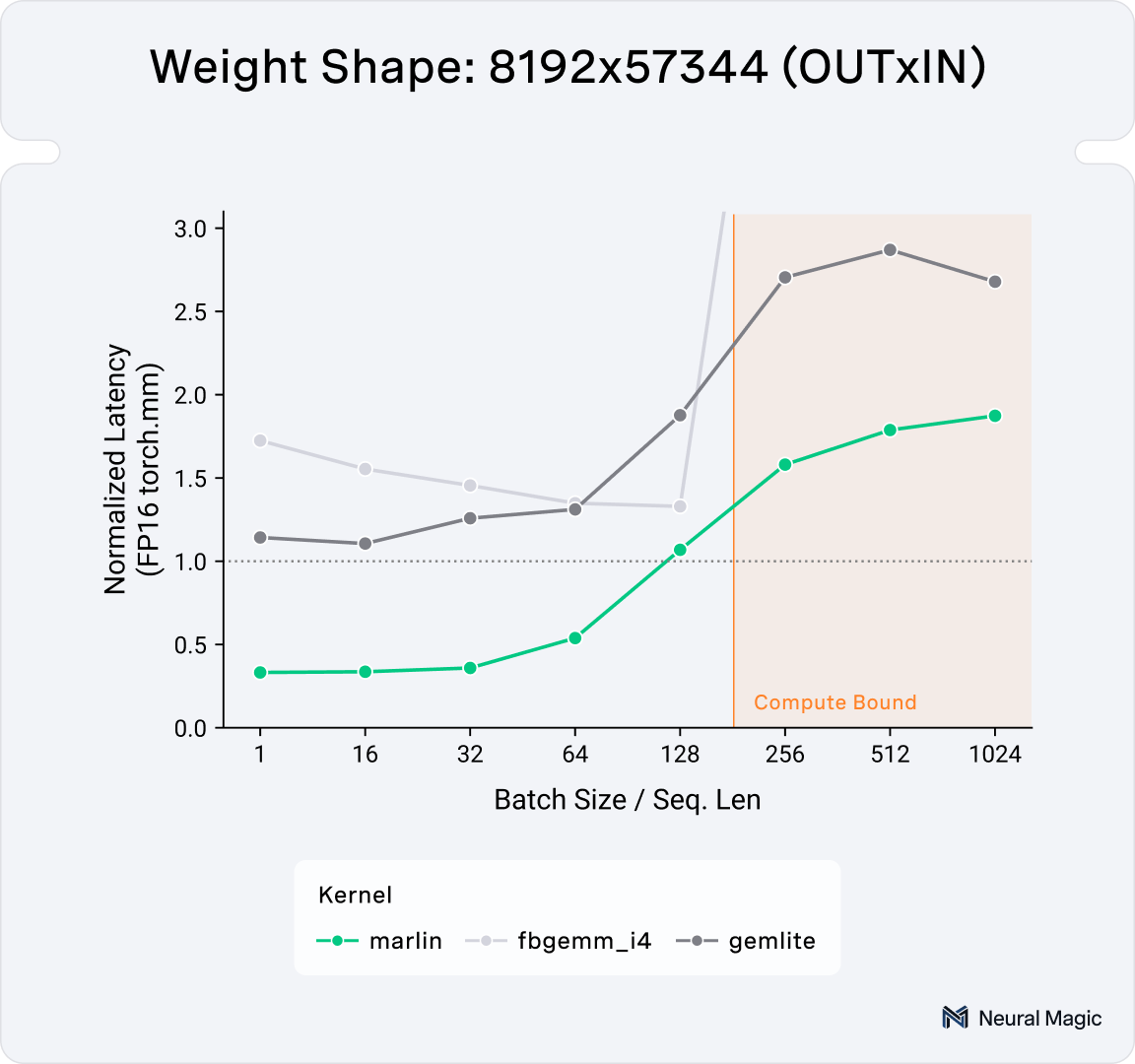
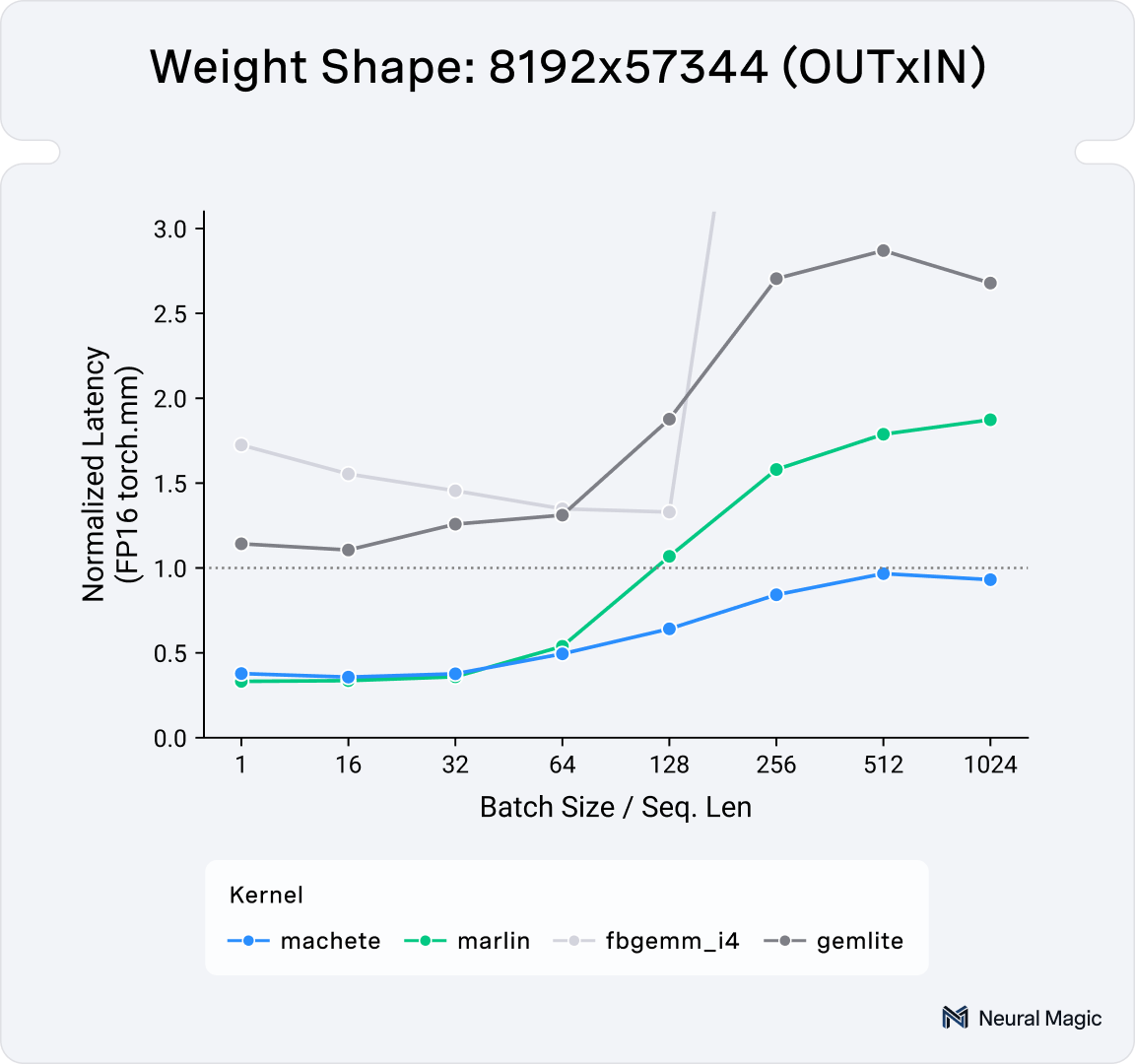
LLM inference involves a mix of both compute-bound and memory-bound iterations. On modern NVIDIA Hopper GPUs, current state-of-the-art mixed-input linear kernels struggle in compute-bound scenarios (as illustrated in Figure 1).
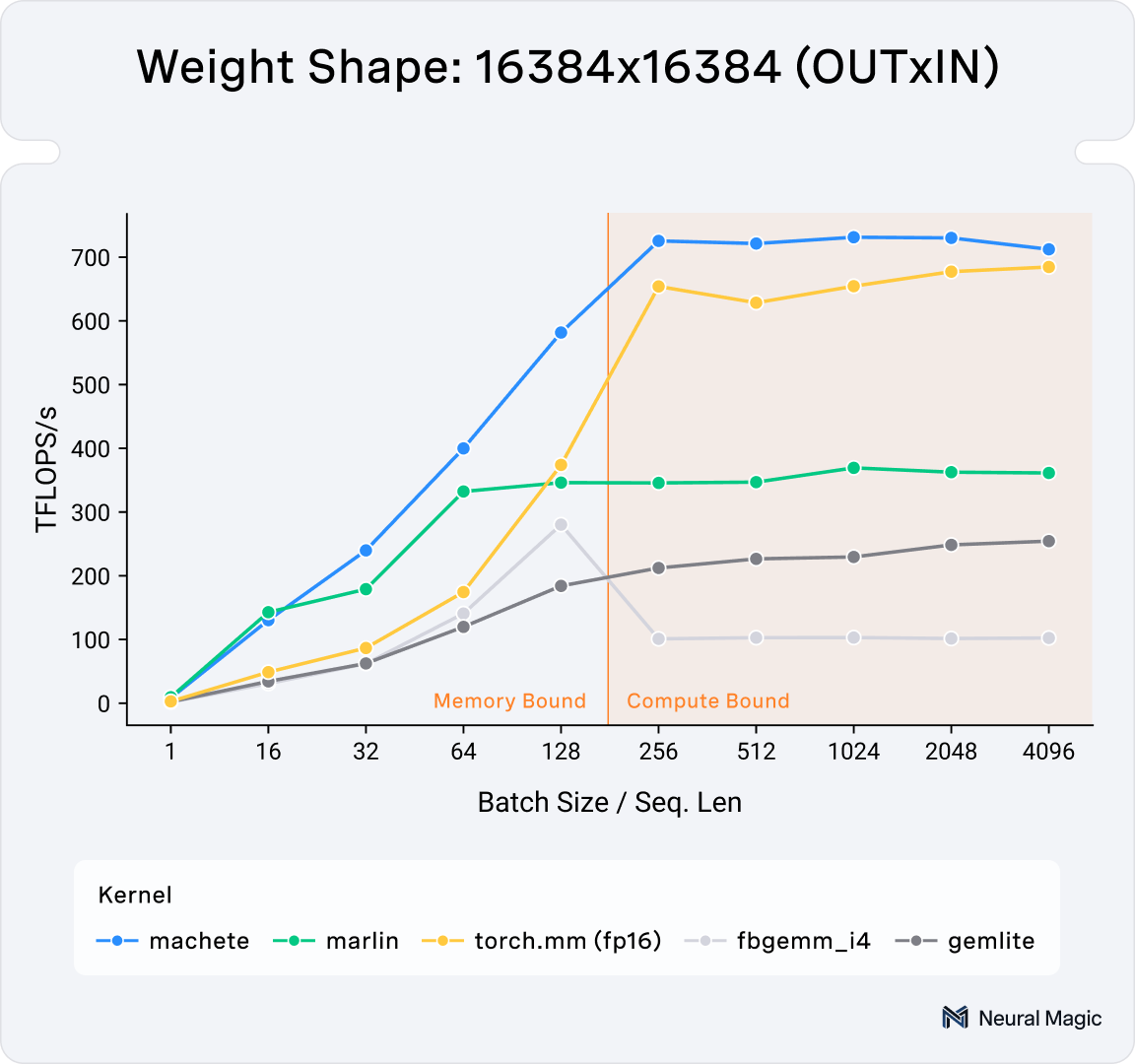
We are excited to announce Machete, Neural Magic's latest advancement in mixed-input quantization performance. This kernel is the spiritual successor to the Marlin kernels created by Elias Frantar and integrated into vLLM by Neural Magic. While Marlin was specifically designed for Ampere generation GPUs and struggles on Hopper GPUs (namely H100), Machete was built on top of the work highlighted in CUTLASS 3.5.1 (see example #55 as our initial starting point). This allows it to efficiently target Hopper and beyond, performing well in both compute and memory-bound regimes. It optimizes the on-the-fly upconversion of weights required in mixed-input scenarios, and hides this latency by overlapping it with compute and data-movement.
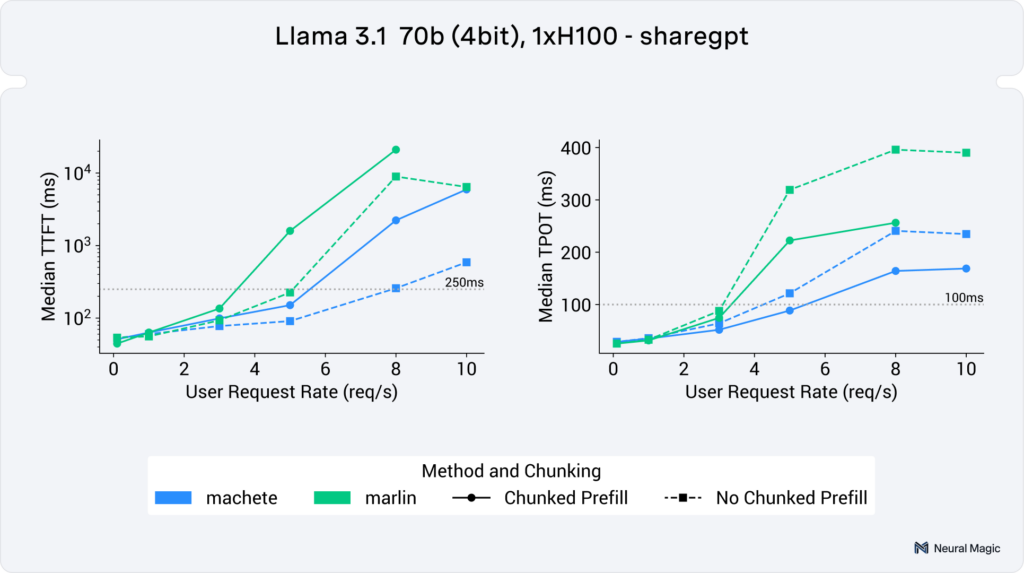
Machete is now available in vLLM 0.6.2+ as a backend for w4a16 and w8a16 compressed-tensors models, for GPTQ models, and more to come. With Machete, you can now serve Llama 3.1 70B on a single H100 GPU with up to 5 user requests per second while maintaining a median time to first token (TTFT) of <250ms and a median time per output token (TPOT) of <100ms (using chunked prefill on the ShareGPT dataset).
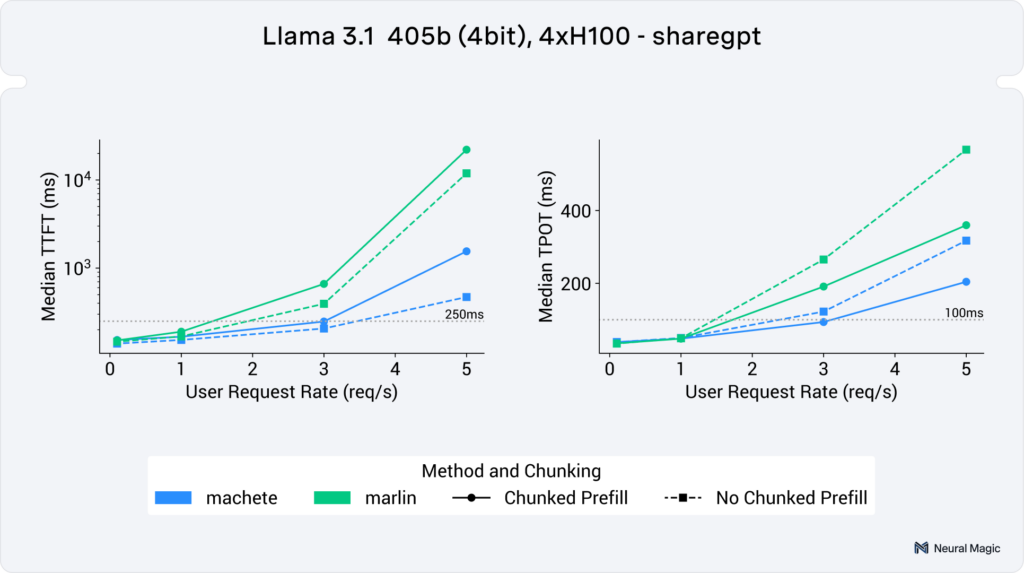
With Machete you can now also hit those same serving targets for Llama 3.1 405B using 4 H100 GPUs with up to 3 user requests per second.
NOTE: Our use of the term "mixed-input" rather than "mixed-precision" is deliberate, as it more accurately describes the specific case we're addressing. The term "mixed-precision" has traditionally been used to describe a broader range of cases, namely including the case where activations and weights share the same type but are accumulated into a different type (i.e. w8a8).
Optimizing Mixed-Input Linear Operations: Weight Pre-Shuffling
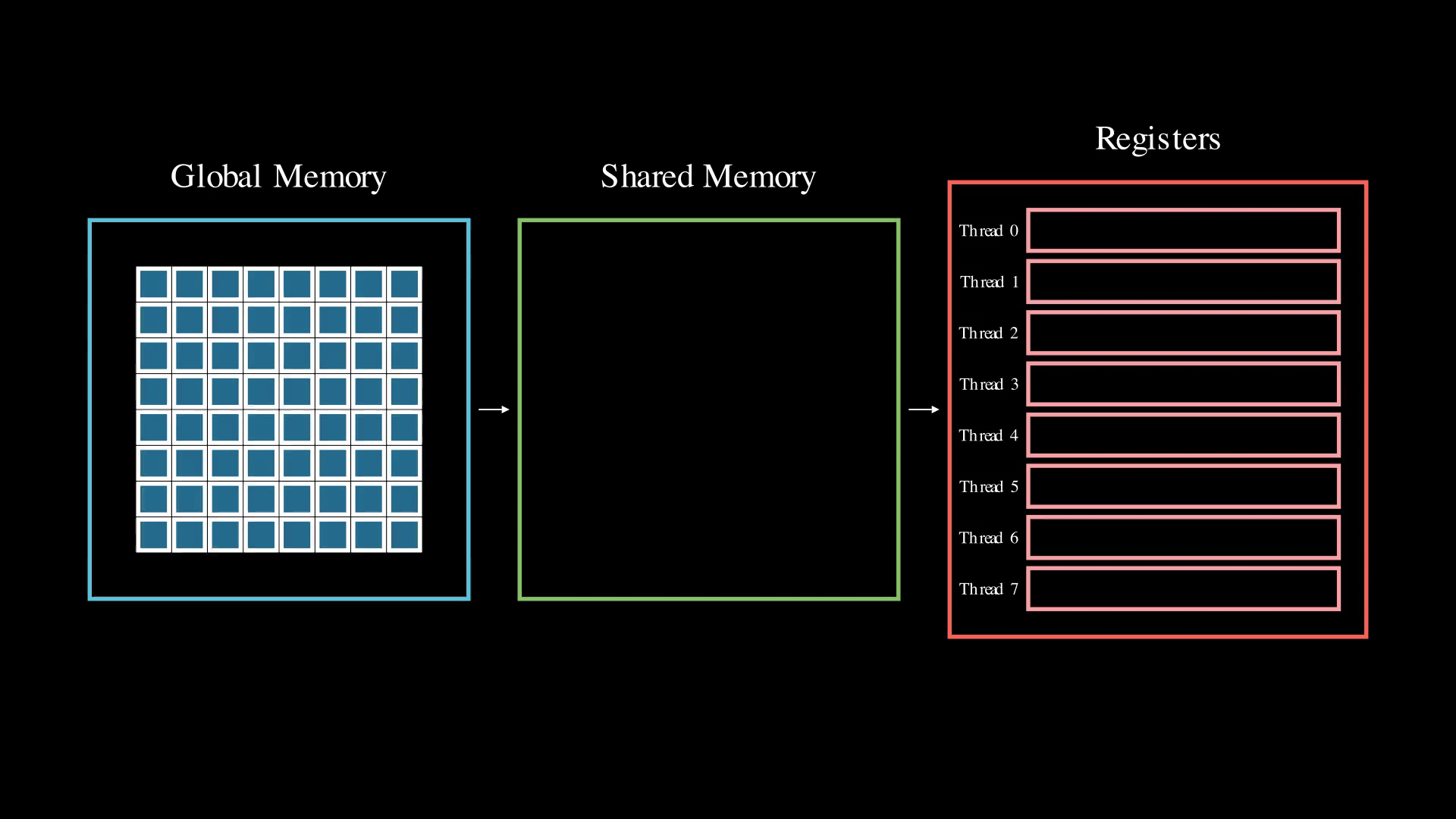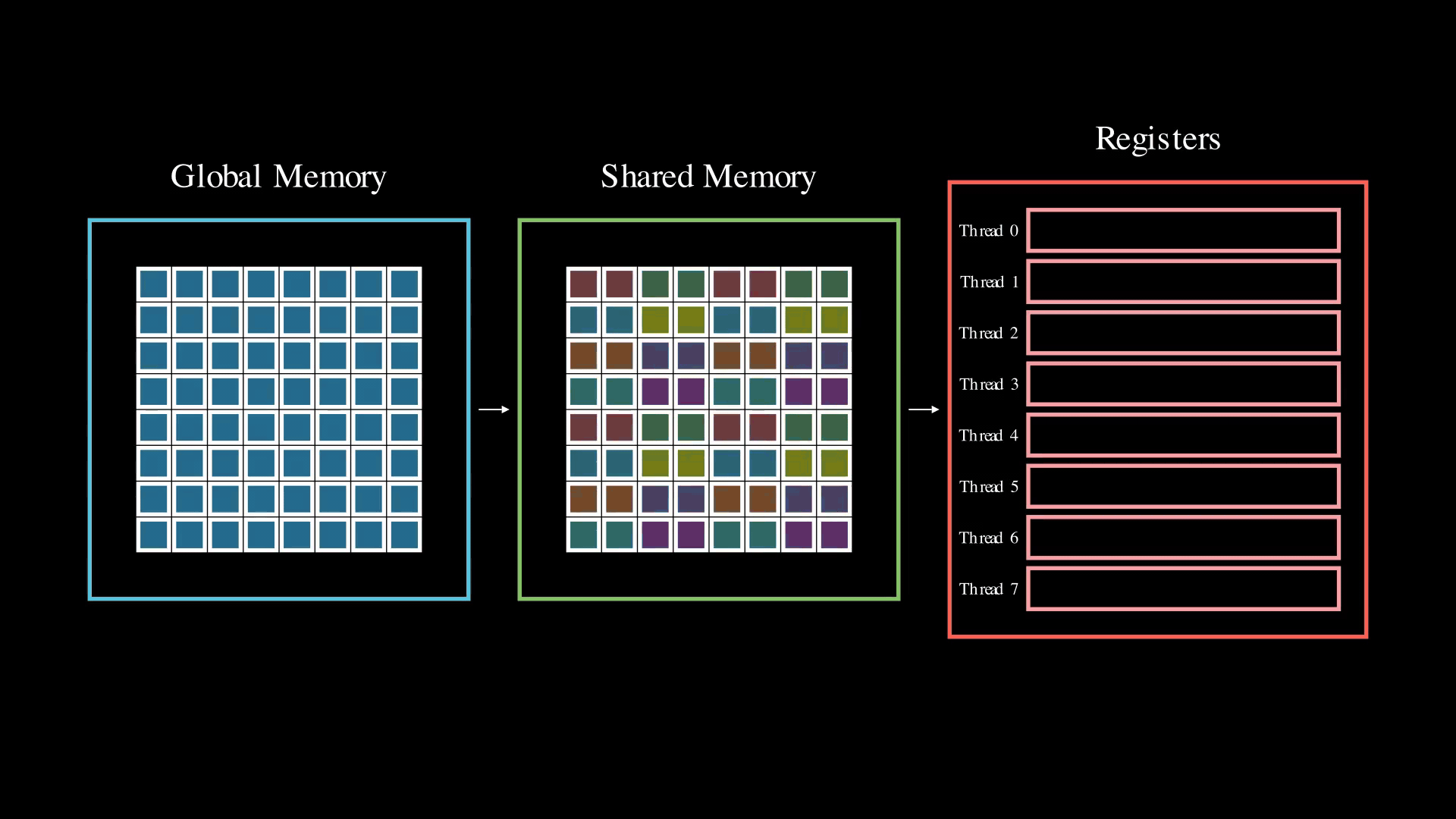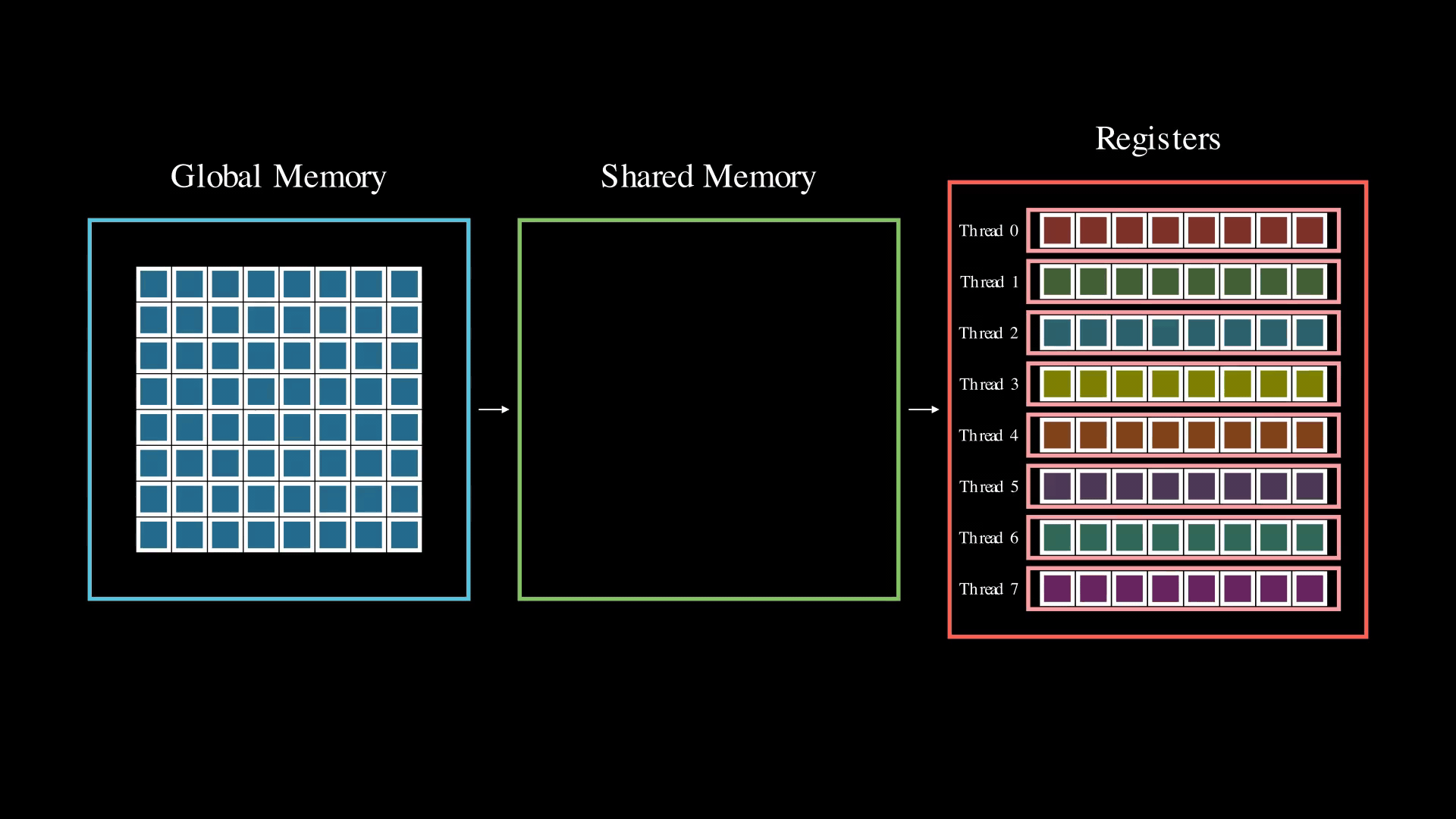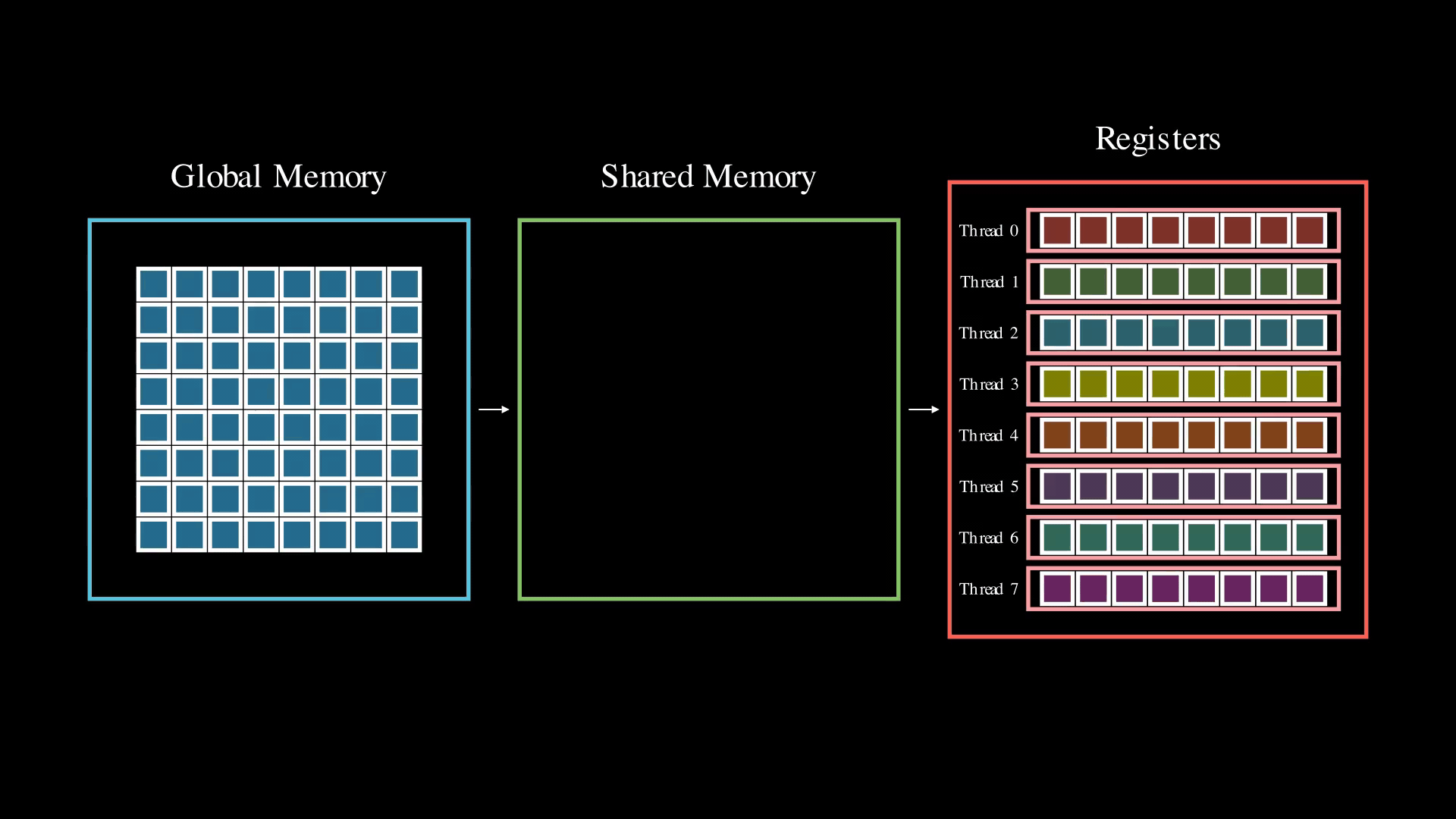
While Neural Magic's previous blog post on Marlin covered many optimizations for mixed-input linear operations, this article focuses on an important previously undiscussed optimization used by both Marlin and Machete: weight pre-shuffling. To understand the benefits of weight pre-shuffling, we first need to examine how data is fed into the tensor cores in NVIDIA GPUs.
When performing matrix-input multiplication on a GPU, the process begins by loading data for a small subproblem from global memory to an SM's local shared memory. This data is then transferred to threads and passed to the tensor cores. Each thread is responsible for loading and holding a specific piece of data in its registers. The layout of this data in registers follows a fixed, complex pattern that varies depending on the instructions used (such as mma or wgmma).
In PyTorch, weights are typically stored in row-major or column-major format, which doesn't align with the intricate layout required by tensor cores. This mismatch creates a challenge: while we can load data into shared memory in row-major format, we must shuffle it when loading into registers to match the tensor core requirements.
For the purposes of illustration in the following animations, we're using a fictitious GPU that has 8 threads per warp and tensor cores that operate on 8x8 chunks of the weight matrix. While simplified, this closely matches the types of layouts used by NVIDIA tensor cores, albeit scaled down. In these diagrams, we only show the weight matrix (and not activations) as loading and up-converting the weight matrix is the main challenge in mixed-input linear layers.
For standard data types (16, and 32-bit), NVIDIA provides an efficient ldmatrix instruction to perform this shuffling in hardware; i.e. ensuring that the right data gets shuffled to the right thread.
However, this instruction isn't available for 4-bit types. When working with 4-bit elements and using float16 or bfloat16 as the compute type, we need to load 4-bit elements to match the thread layout for a 16-bit type. Without a 4-bit ldmatrix instruction, we would naively need to resort to performing four 8-bit shared memory loads per tensor core operation. In this case the data shuffling is being handled by software using multiple shared memory loads. These additional shared memory loads are detrimental to performance, as they add latency and the use of only 8-bit loads restricts the shared-memory to registers bandwidth.
To overcome this limitation, we can reorder the data ahead of time. By doing so, we can perform a single 32-bit load from shared memory instead of four 8-bit loads. This approach is much more efficient in terms of shared memory bandwidth and latency, ensuring we don't get bottlenecked waiting for shared memory. Importantly, all global memory reordering is done in advance, so it doesn't impact inference time. This pre-shuffling and its effect on how the data gets loaded into memory can be seen in Animation 3.
We can push this optimization even further. By interleaving data for four tensor operations together (e.g., interleaving four 8x8 tiles in the visualization), we can perform 128-bit loads—the widest shared load instruction currently available on CUDA devices.
After loading the weight parameters into the correct registers, they must be upconverted to 16-bit. Animation 5 demonstrates this process, highlighting how the interleaving of tiles can simplify upconversion and save instructions. By interleaving tiles in global memory, the data is arranged so that, once in registers, multiple nibbles can be efficiently extracted and up-converted in parallel. This is achieved by shifting the nibbles into the lower four bits of their destination registers using simple bit shifts and masking operations and then expanding in-place. If you're curious about these interleaved upconverts, you can find them here.
What's New in Machete vs. Marlin?
These types of repackaging techniques have already been used in previous mixed-input kernels (namely Marlin and AWQ), so what does Machete do differently? The motivation for developing Machete mainly stems from the poor performance of current mixed-input linear kernels on the NVIDIA Hopper architecture when it comes to larger, more compute bound matrix-multiplications, as can be seen in Figure 1.
New Tensor Core Instructions (wgmma)
For Marlin, the poor performance on Hopper architecture primarily stems from the use of outdated 'mma' tensor core operations. To achieve peak FLOPs on NVIDIA Hopper, the new 'wgmma' instructions must be utilized. Using only 'mma' instructions results in a loss of approximately 37% of peak compute throughput [1, 2].
Marlin's weight pre-shuffling, being hand-derived and implemented, makes it challenging to easily adapt to the new 'wgmma' layouts. Machete circumvents this issue by employing CUTLASS CUTE layout algebra to construct a description of the repacked layout for a full weight matrix using instruction layout definitions available in CUTLASS. This approach should, in theory, facilitate easier adaptation to any future instructions as well as different types (w4a8 is already in progress).
A key challenge with 'wgmma' is that for a matrix multiplication C = AB, only A and C can be sourced from registers, while B must be sourced from shared memory. Since we upconvert the 4-bit bit weights to 16-bit floating point values in registers, we can avoid restoring them into shared memory by computing Y^T = W^T * X^T instead of Y = XW. This ensures the weights are ‘A’ (left side input-operand) with respect to the ‘wgmma’ instructions, allowing them to be sourced directly from registers. CUTLASS enables us to more easily compute the transpose problem by simply manipulating layouts.
Tensor Memory Accelerator (TMA)
The Tensor Memory Accelerator (TMA) represents a significant advancement in NVIDIA Hopper GPUs' memory handling capabilities. This new hardware feature is designed to asynchronously copy blocks of multidimensional data, known as subtensors, from global memory to shared memory. The introduction of TMA brings several important benefits to the table.
Primarily, TMA reduces register pressure by offloading data movement operations, thereby freeing up CUDA cores for other computational tasks. It also simplifies address calculations by handling these complex operations in hardware. Furthermore, TMA's ability to operate independently of compute operations allows for better overlap between memory transfers and computations. Machete takes advantage of this new hardware feature by leveraging CUTLASS's existing TMA infrastructure.
Warp-specialization
Warp-specialization, introduced in CUTLASS 3.0, divides warps into data movement (producer) and computation (consumer) roles. This technique aims to better overlap data movement and computation, improving memory and tensor core latency hiding. Machete incorporates this approach by leveraging existing infrastructure in CUTLASS. For a more detailed explanation of warp-specialization in CUTLASS, refer to this COLFAX Research blog.
Machete Performance
With all of the above optimizations in place, we can see that Machete outperforms the other mixed input linear kernels for batch size / prefill seq. len 128+. At batch sizes of 128 and above, the performance is competitive with FP16, meaning there is no longer a trade-off between prefill performance or high-batch size performance and improved low-batch and decode performance.
In Figure 6 we can see end-to-end serving performance of these kernels on a 4bit Llama 3.1 70B on a single H100. In the higher user requests rates (3+ req/s), we see a geomean speedup of 29% for input token throughput and 32% for output token throughput.
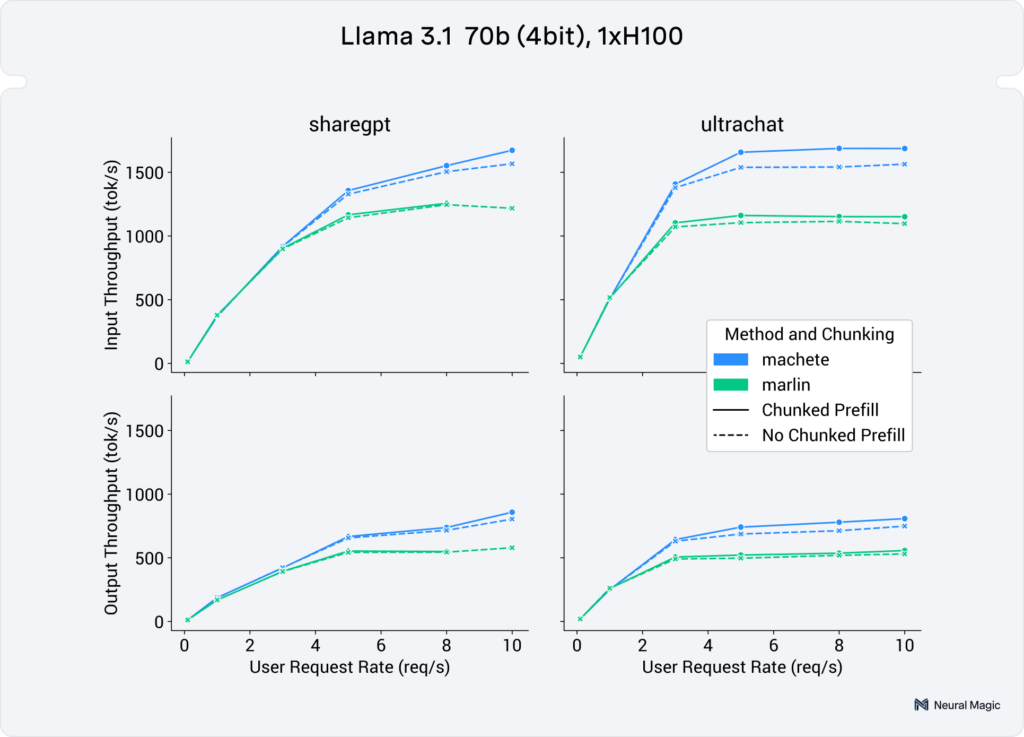
(neuralmagic/Meta-Llama-3.1-70B-Instruct-quantized.w4a16)
In Figure 7 we can see end-to-end serving performance of these kernels on a 4bit Llama 3.1 405b on 4 H100s. In the higher user requests rates (3+ req/s),we see a geomean speedup of 42% for both input token and output token throughput.
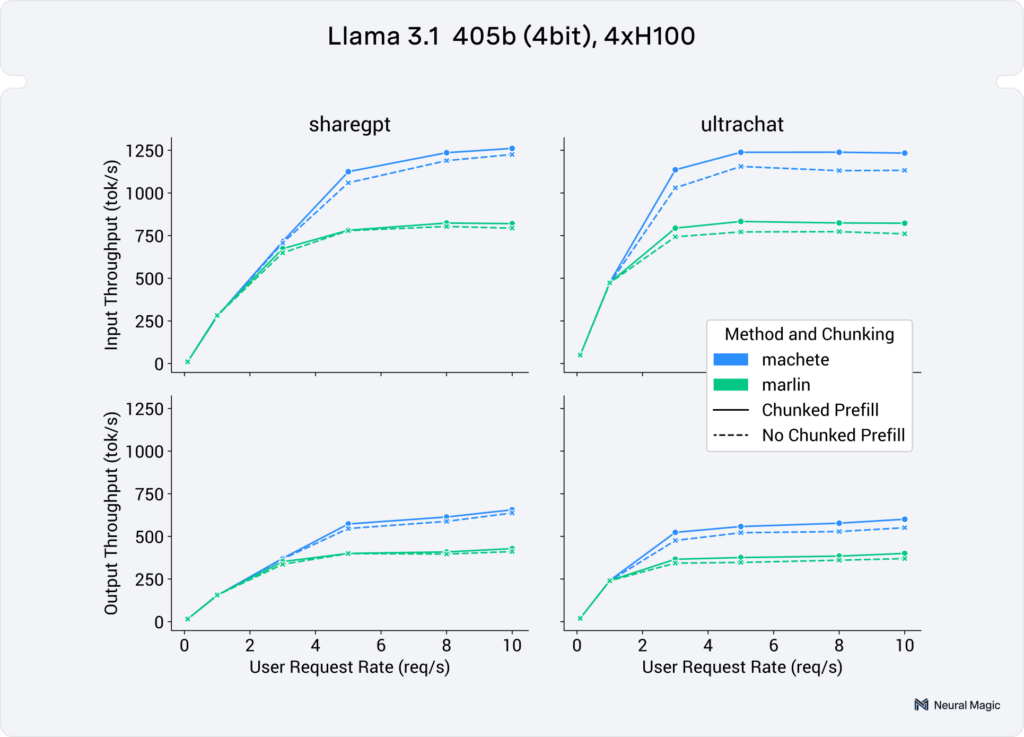
(neuralmagic/Meta-Llama-3.1-405B-Instruct-quantized.w4a16)
Future Work
As we continue to develop and refine Machete, we have several exciting areas of focus for future improvements:
- w4a8 FP8 Support: We are experimenting with w4a8 FP8 to achieve the memory savings of 4-bit weights while leveraging FP8 activations for improved compute throughput.
- Broadening Quantization Method Support: We plan to extend support for additional quantization techniques, such as AWQ and QQQ, which are already integrated into vLLM, beyond the current GPTQ-style support.
- Introducing LUT-Based Quantization Schemes: We are working to expand Machete's capabilities by incorporating lookup table (LUT) based quantization methods, including NF4.
- Optimizing Low Batch Size Performance: We will continue to focus on optimizing performance for low batch sizes (sub-32).
These initiatives underscore our commitment to pushing the boundaries of mixed-input quantization performance. By addressing these areas, we aim to make Machete an even more powerful and flexible tool for efficient LLM inference on NVIDIA Hopper GPUs and beyond. We're excited about the potential impact of these improvements and look forward to sharing updates as we progress. Subscribe to our blog, follow us on X, and join our bi-weekly vLLM office hours to stay tuned for more exciting AI developments.
About Neural Magic
Neural Magic is advancing the performance of AI inference by optimizing large language models (LLMs) for efficient and scalable deployments. As a leading contributor to the open-source vLLM project, we develop and implement key techniques like sparse architectures, mixed-precision quantization, and performance optimizations to enhance inference speed, reduce memory footprint, and maintain model accuracy. Neural Magic is also a member of NVIDIA Inception, a program designed to nurture startups, and is thankful to the CUTLASS team for their valuable work. Our goal is to empower developers to build and deploy high-performance LLMs across different hardware configurations without compromise. To learn more, visit neuralmagic.com or check out our GitHub to accelerate your AI workloads today.






