Pushing the Boundaries of Mixed-Precision LLM Inference With Marlin

In the rapidly evolving landscape of large language model (LLM) inference, the quest for speed and efficiency on modern GPUs has become a critical challenge. Enter Marlin, a groundbreaking Mixed Auto-Regressive Linear kernel that unlocks unprecedented performance for FP16xINT4 matrix multiplications. Developed by Elias Frantar at IST-DASLab and named after one of the planet's fastest fish, the mixed-precision LLM inference kernel, Marlin, delivers ideal 4x speedups for batch sizes up to 32 tokens, a significant leap from the limited speedup offered only at batch_size=1 achieved with prior work. This makes Marlin an exceptional choice for larger-scale serving, speculative decoding, and advanced multi-inference schemes. Neural Magic has integrated and expanded upon Marlin in nm-vllm for optimal LLM serving on GPUs.

In this blog post, we will dive deep into the technical innovations that power Marlin's remarkable LLM inference performance. We'll explore the challenges of optimizing inference kernels for modern GPUs and dissect the key techniques and optimizations employed by Marlin to achieve its unparalleled efficiency.

Background on Mixed-Precision LLM Inference

Mixed-precision LLM inference computing is a game-changer for machine learning. By leveraging a combination of different numerical precisions, mixed-precision inference allows for reduced memory footprint and the potential for significant speedups without compromising accuracy.

Quantizing weights is easier than quantizing activations because weights remain constant during inference, while activations change dynamically based on the input. This static nature of weights allows for a simpler quantization process, as the optimal quantization parameters can be determined offline and applied consistently during inference. Quantizing activations, on the other hand, requires real-time quantization during inference, which is more challenging due to the dynamic range and distribution of activation values. Additionally, the impact of quantization errors on activations can propagate through the network, potentially leading to more significant accuracy degradation compared to weight quantization. Therefore, weight quantization is often preferred as a more straightforward approach to reduce model size in LLMs.

GPTQ is an industry-leading one-shot weight quantization method based on approximate second-order information, that is both highly accurate and highly efficient. Methods like GPTQ compress weights from 16-bits to 4-bits while only slightly affecting accuracy. However, realizing the full potential of mixed-precision LLM inference has traditionally been hindered by performance bottlenecks and suboptimal utilization of GPU resources. While b=1 latency is excellent when there is ample compute available to maximize effective memory bandwidth for 4-bit weights, achieving a hopeful 4x speedup over FP16 weights, this poor utilization of compute renders mixed-precision a suboptimal solution for LLM serving with multiple users. This is where Marlin comes in, broadening the effective range of mixed-precision LLM inference.

Why Marlin is State-of-the-Art for Mixed-Precision LLM Inference

Marlin's architecture leverages a crucial observation: modern GPUs typically exhibit floating-point operations (FLOPs) to byte ratios ranging from 100 to 200. Consequently, as long as fewer than 25-50 tensor core multiply-accumulate operations are performed per 4-bit quantized weight, it is feasible to maintain a near-optimal 4x speedup compared to FP16 weights. This implies that the complete performance advantages of weight-only quantization should theoretically be applicable to batch sizes 4-8x larger than those currently achieved by existing methods.

The graph below, from the original overview, compares the performance of Marlin with other widely-used 4-bit inference kernels on a large matrix that can be optimally partitioned on an NVIDIA A10 GPU. All kernels are executed at a groupsize of 128, although it should be noted that scale formats are not entirely identical.

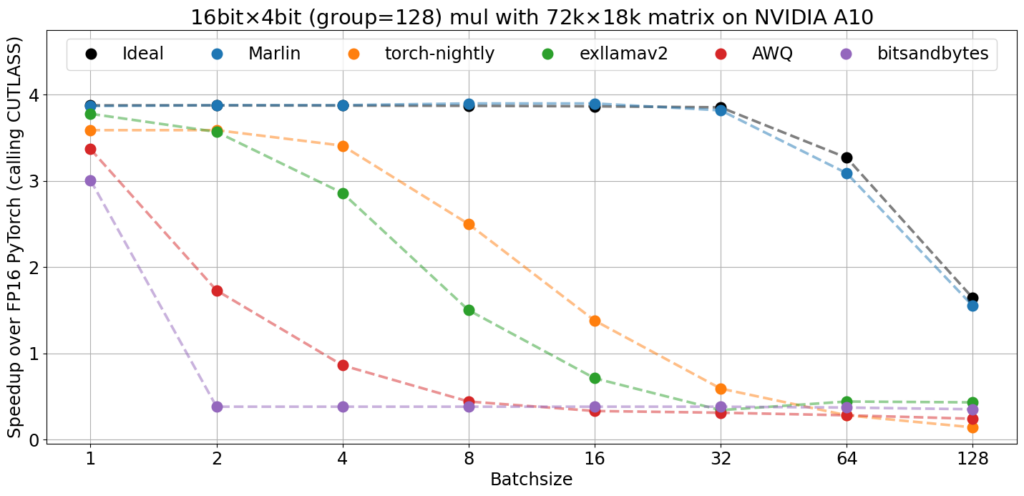
Existing kernels attain relatively close to the optimal 3.87x speedup (taking into account the 0.125 bits storage overhead of the group scales) at batch size 1. However, their performance rapidly deteriorates as the number of tokens increases. In contrast, Marlin consistently delivers near-ideal speedups across all batch sizes, enabling the maximum achievable 3.87x speedup for batch sizes up to approximately 16-32. 

Mixed-Precision LLM Inference Key Techniques and Optimizations

Marlin optimizes GPU resources like global memory, L2 cache, shared memory, vector cores, and tensor cores simultaneously. It accomplishes this through various techniques:

1. Asynchronous Global Weight Loads
2. Circular Shared Memory Queue
3. Task Scheduling and Synchronization

Let’s explore these techniques in more detail.

Asynchronous Global Weight Loads

Marlin takes advantage of the asynchronous data movement capabilities introduced in the NVIDIA Ampere architecture to optimize loading of weights from global memory. By using the cuda::memcpy_async API, Marlin initiates non-blocking copies of neural network weights directly into shared memory. This technique does not require the utilization of threads or registers to manage the data transfer, allowing these resources to remain fully dedicated to computational tasks. This concurrent execution model enables Marlin to overlap weight transfer with ongoing computations, effectively masking the latency traditionally associated with accessing global memory.

A pipelined processing strategy further refines this approach. Marlin orchestrates the prefetching of weights using cuda::pipeline to fetch weights for the upcoming subset N+1, while simultaneously performing computations on the current subset N. This pipelined prefetching is important in maintaining a constant flow of computation, hiding much of the latency of the global memory accesses. Moreover, this method of asynchronous weight loading is designed to mitigate the impact on the L2 cache. By bypassing the L2 cache and transferring weights directly to shared memory, Marlin preserves the cache's capacity for storing input and output activations, thereby enhancing overall cache utilization and performance efficiency.

// Asynchronously fetch the next A, B and s tile from global to the next shared memory pipeline location.
auto fetch_to_shared = [&] (int pipe, int a_off, bool pred = true) {
  if (pred) {
    int4* sh_a_stage = sh_a + a_sh_stage * pipe;
    #pragma unroll
    for (int i = 0; i < a_sh_wr_iters; i++) {
      cp_async4_pred(
        &sh_a_stage[a_sh_wr_trans[i]],
        &A[a_gl_rd_delta_i * i + a_gl_rd + a_gl_rd_delta_o * a_off],
        a_sh_wr_pred[i]
      );
    }
    int4* sh_b_stage = sh_b + b_sh_stage * pipe;
    #pragma unroll
    for (int i = 0; i < b_sh_wr_iters; i++) {
      cp_async4_stream(&sh_b_stage[b_sh_wr_delta * i + b_sh_wr], B_ptr[i]);
      B_ptr[i] += b_gl_rd_delta_o;
    }
    // Only fetch scales if this tile starts a new group
    if (group_blocks != -1 && pipe % (group_blocks / thread_k_blocks) == 0) {
      int4* sh_s_stage = sh_s + s_sh_stage * pipe;
      if (s_sh_wr_pred)
        cp_async4_stream(&sh_s_stage[s_sh_wr], &s[s_gl_rd]);
      s_gl_rd += s_gl_rd_delta;
    }
  }
  // Insert a fence even when we are winding down the pipeline to ensure that waiting is also correct at this point.
  cp_async_fence();
};

Circular Shared Memory Queue

Marlin incorporates multiple shared memory buffers to create a cyclic buffer system. This system is designed to efficiently manage the loading and usage of data in shared memory, allowing for a continuous cycle of loading, processing, and unloading of data without the need for synchronization points that would otherwise stall computation.

The architecture of this circular queue involves multiple shared memory buffers, enabling Marlin to preload data into subsequent buffers while computations are being performed on the current buffer. This strategy significantly increases the throughput of data processing by ensuring that computation and data loading can occur simultaneously without interference. The use of a circular buffer mechanism allows for a transition between buffers, where each buffer is dynamically assigned as the next target for data loading or the current source for computation based on the cycle's position.

// Register storage for double buffer of shared memory reads. 
FragA frag_a[2][thread_m_blocks];
I4 frag_b_quant[2];
FragC frag_c[thread_m_blocks][4][2];
FragS frag_s[2][4];
…
// Wait until the next thread tile has been loaded to shared memory.
auto wait_for_stage = [&] () {
  // We only have `stages - 2` active fetches since we are double buffering and can only issue the next fetch when
  // it is guaranteed that the previous shared memory load is fully complete (as it may otherwise be overwritten).
  cp_async_wait<stages - 2>();
  __syncthreads();
};

Task Scheduling and Synchronization

Marlin employs a highly efficient task scheduling and synchronization strategy to maximize the utilization of GPU resources during matrix multiplication, particularly the streaming multiprocessors (SMs). At the core of this strategy lies the Stream-K parallelization approach, which involves uniform partitioning of the problem M and N dimensions and non-uniform partitioning along the K dimension.

To illustrate this concept, consider an example of a matrix multiplication (C = AxB) with a problem shape of 32x512x4096 (MxNxK). By partitioning M and N uniformly by factors of 1 and 4, respectively, we obtain 4 equally sized (32x128) output tiles labeled 0-3, as shown in the figure below.

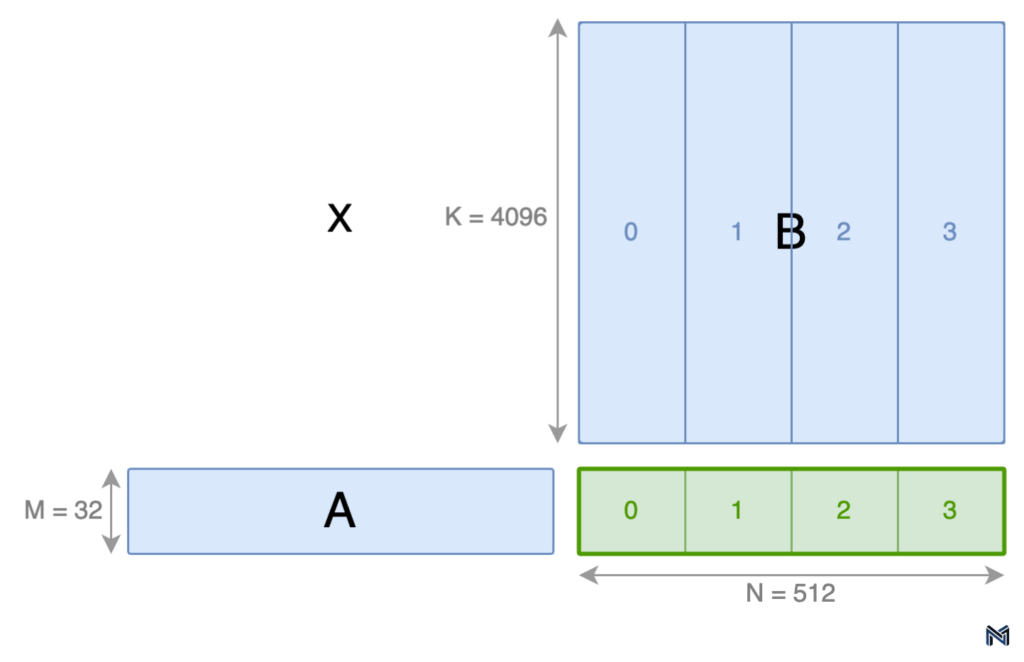
However, uniform partitioning along the K dimension can lead to suboptimal utilization of SMs. In the case of our example, consider a fictitious GPU with 6 SMs. If we were to partition K uniformly, only 4 of the available SMs would be assigned an output tile, leaving the remaining 2 SMs idle. This inefficiency highlights the need for a more sophisticated approach to work distribution.

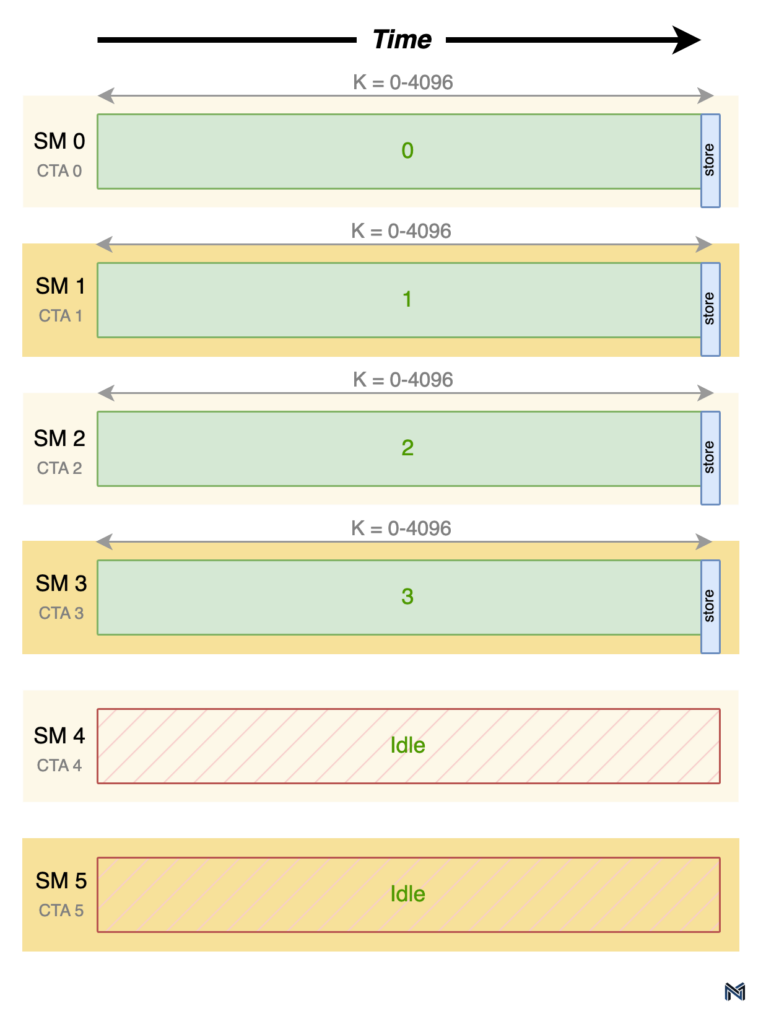
Marlin addresses this issue by employing a non-uniform partitioning scheme along the K dimension. In this approach, the work is scheduled on a GPU with multiple SMs by launching one collective thread array (CTA) per SM. Each CTA then attempts to grab an equal chunk of work, with CTA 0 going first, followed by CTA 1, and so on. Partitions along the K dimension result in multiple SMs contributing partial results to the same output tile, necessitating synchronization between the SMs and a reduction of the partial results.

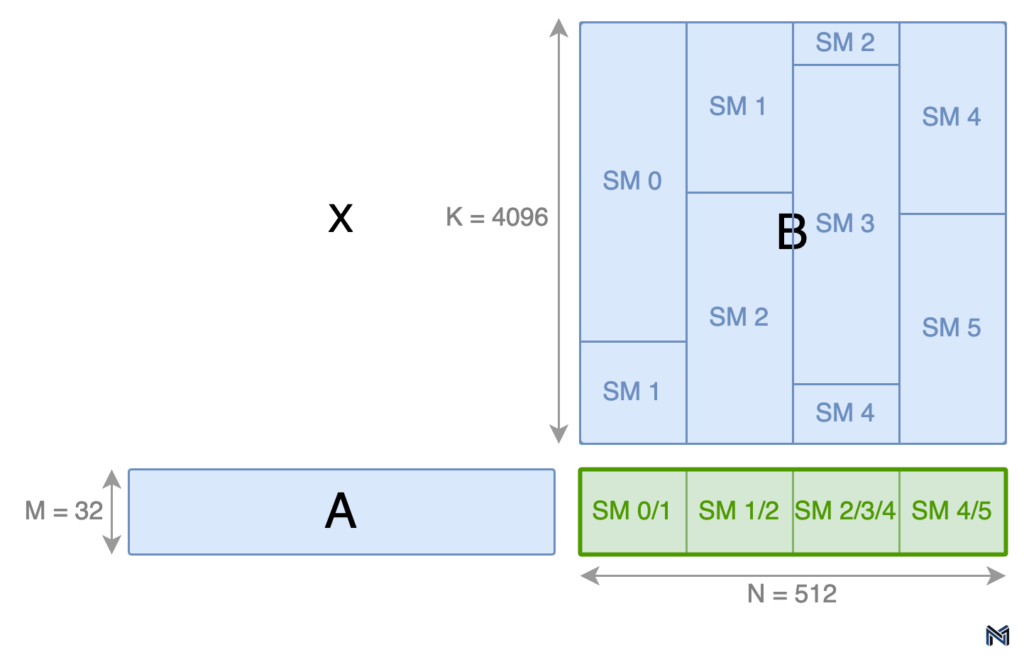
To minimize excessive synchronization overhead, Marlin allocates work from each output tile sequentially. In other words, all of the work for output tile 0 is scheduled before moving on to output tile 1, and so on. This sequential allocation ensures that the synchronization and reduction operations are performed efficiently. The timeline diagram below illustrates the work performed by each SM, with the green numbers representing the output tile being worked on.

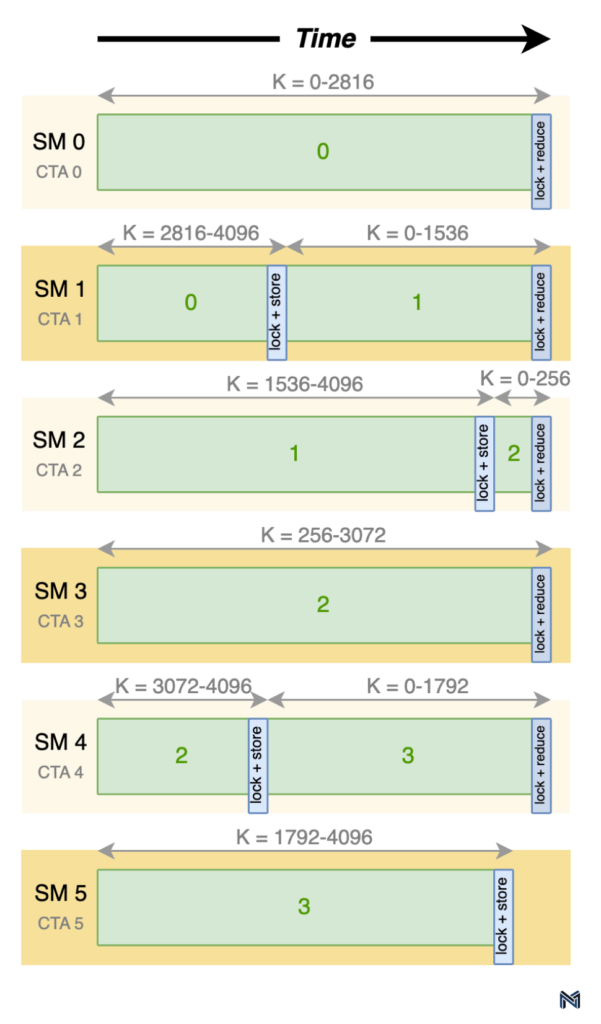
As evident from the timeline, the first SM to complete a partial result for an output tile stores the partial result in global memory, locking that portion of the output buffer until the write operation is complete. The next SM to produce a partial result then adds its contribution to the partial result already present in global memory, again locking the corresponding portion of the output buffer during the process.

A key advantage of Marlin's approach is its ability to leverage the L2 cache for efficient partial result reductions. During the decoding phase of LLM inference, which is the primary target of Marlin, the size of the output is relatively small. By ensuring that the output fits into the L2 cache, Marlin significantly speeds up the partial result reduction operations, minimizing the performance impact of synchronization.

By combining the Stream-K parallelization approach with intelligent work allocation, efficient synchronization, and effective utilization of the L2 cache, Marlin achieves optimal performance and scalability across a wide range of GPU architectures and problem sizes. This sophisticated task scheduling and synchronization strategy is a critical component of Marlin's ability to deliver close to ideal speedups for larger batch sizes in mixed-precision LLM inference.

Implications for Real-World Applications

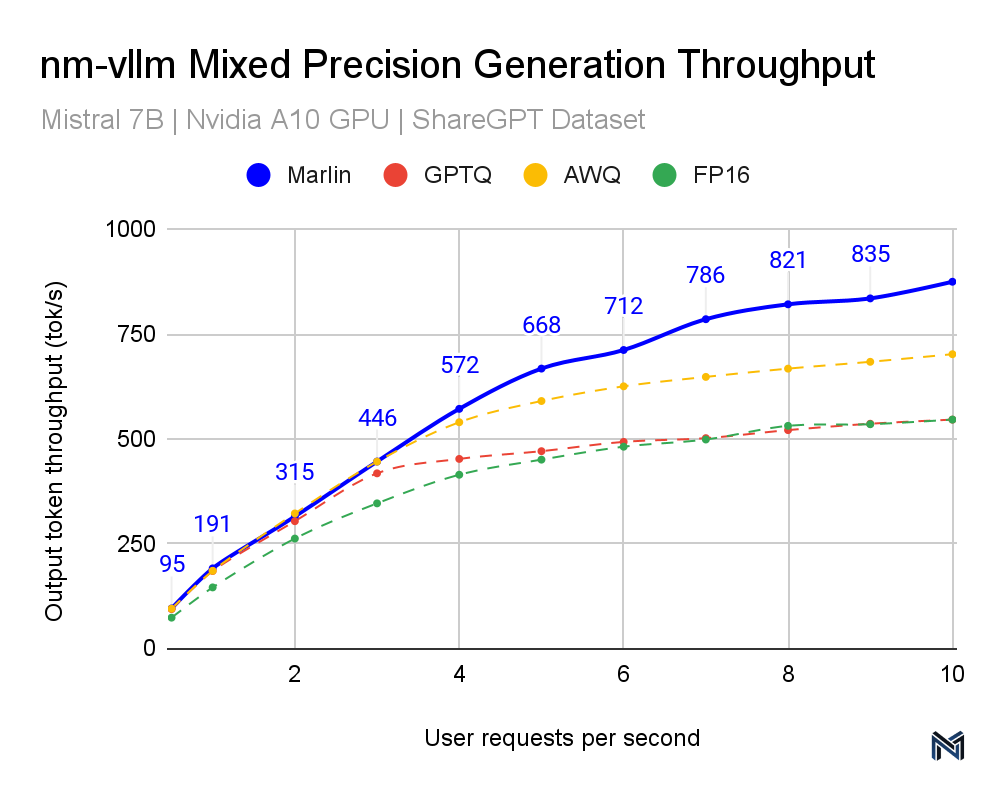
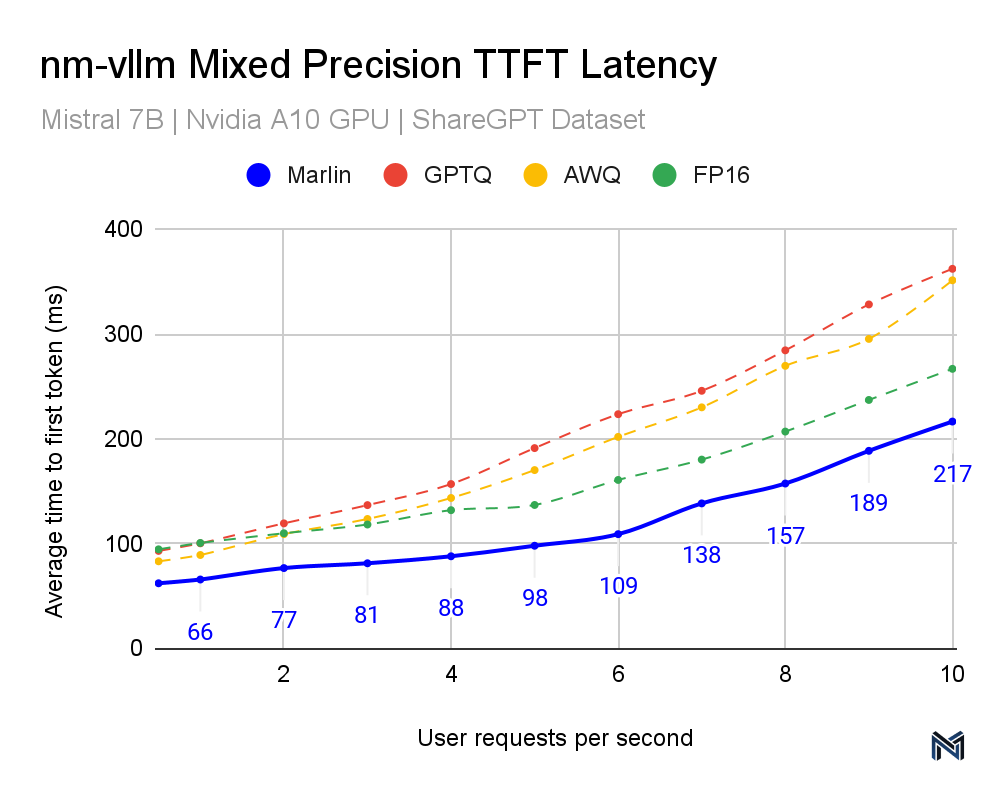
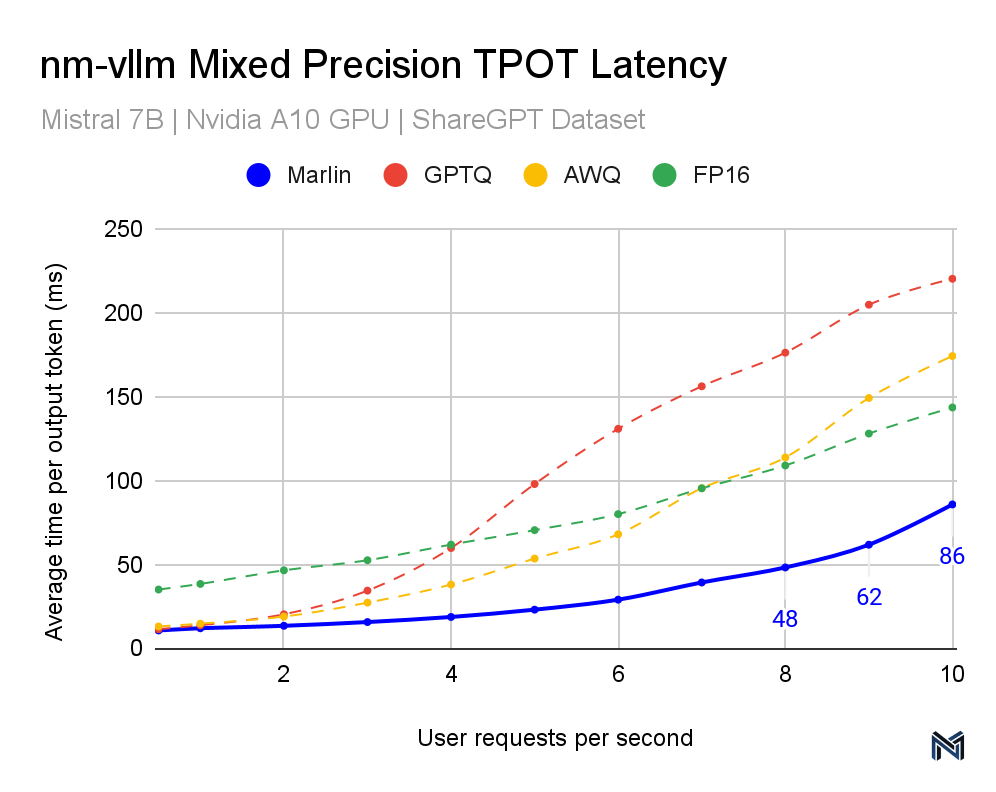
Marlin's performance across various inference schemes is noteworthy, positioning it as a superior solution in the landscape of mixed-precision LLM inference. This distinction is evident in the data provided in the accompanying graphs. Both the TTFT (Time To First Token) and TPOT (Time Per Output Token) latency measurements indicate that Marlin outperforms other methods, particularly at higher queries per second (QPS). As the QPS increases, representing higher demand and throughput scenarios typical in real-world applications, Marlin maintains a lower latency compared to the other methods tested, including GPTQ, AWQ, and FP16, showcasing the most efficient utilization of computational resources.

Specifically, for the TTFT latency at 10 QPS, Marlin achieves about 217ms, while the nearest competitor method hovers around 300ms. Similarly, for the TPOT latency, Marlin maintains a latency of 86ms at 10 QPS, significantly outpacing other methods that approach or exceed 200ms. These results are crucial for performance engineers because they illustrate how Marlin can sustain near-optimal speedups and efficient GPU utilization even as demand increases.

For a guide of how to compress models to 4-bit weights using GPTQ in order to run with Marlin and nm-vllm for lower memory usage and latency, follow this notebook.

Conclusion

Marlin represents a groundbreaking advancement in the realm of mixed-precision LLM inference, pushing the boundaries of performance and efficiency on modern GPUs. The implications of Marlin's performance gains are far-reaching, particularly in real-world applications where high throughput and low latency are critical. As demonstrated by the TTFT and TPOT latency measurements, Marlin maintains its performance edge even under increased demand, making it an ideal solution for performance engineers seeking to optimize LLM inference in production environments.

For those interested in delving deeper into the inner workings of Marlin, we highly recommend exploring the CUDA code snippets provided in Marlin's repository. These code samples offer valuable insights into the implementation details and serve as a starting point for hands-on experimentation and customization.

As the field of AI and deep learning continues to evolve, it is essential to engage with the community and stay abreast of the latest developments in GPU optimizations. Collaborating with fellow researchers, engineers, and enthusiasts can provide valuable insights, practical advice, and opportunities for further innovation. Join the conversation in the Neural Magic Community about all things compression!

In conclusion, Marlin represents a significant milestone in the quest for optimal LLM inference performance. By embracing the techniques and optimizations pioneered by Marlin, developers and researchers can unlock new possibilities in mixed-precision computing, enabling more efficient and scalable AI solutions across a wide range of domains. As we look to the future, Marlin serves as a powerful tool and a source of inspiration for those seeking to push the boundaries of what is possible in the ever-evolving landscape of AI and deep learning.